Tablet beat Pythagoras by a millennium, may explain how the ancients built pyramids
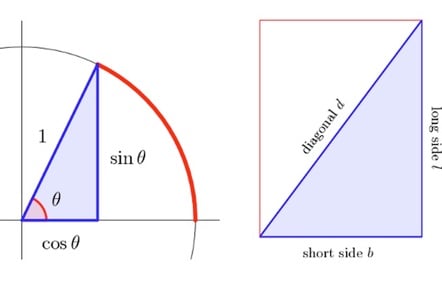
Greek vs. Babylonian triangle workings-out
Those of you who can remember trigonometry can feel free to forget it, because ancient Babylonian mathematicians had a better way of doing it – using base 60!
That's the conclusion of a new paper, Plimpton 322 is Babylonian exact sexagesimal trigonometry, in the new issue of the journal Historia Mathematica.
The “Plimpton 322” from the title is a clay tablet inscribed with cuneiform script. Discovered in the early 1900s, the tablet has been of interest to mathematicians for years because it describes Pythagoras' theorem, yet is thought to have been created around 1800BC, more than a thousand years before Pythagoras was born and started tinkering with triangles.
The rest of the tablet's four columns and fifteen rows of numbers have been debated for some time, but in the paper Daniel Mansfield and N.J. Wildberger, both of the University of New South Wales' School of Mathematics and Statistics, suggest it was a trigonometric table..."
Read on!
That's the conclusion of a new paper, Plimpton 322 is Babylonian exact sexagesimal trigonometry, in the new issue of the journal Historia Mathematica.
The “Plimpton 322” from the title is a clay tablet inscribed with cuneiform script. Discovered in the early 1900s, the tablet has been of interest to mathematicians for years because it describes Pythagoras' theorem, yet is thought to have been created around 1800BC, more than a thousand years before Pythagoras was born and started tinkering with triangles.
The rest of the tablet's four columns and fifteen rows of numbers have been debated for some time, but in the paper Daniel Mansfield and N.J. Wildberger, both of the University of New South Wales' School of Mathematics and Statistics, suggest it was a trigonometric table..."
Read on!
2 comments:
If you add a string of 60 numbers by dropping the "carried" number ( for example, 5 +5 = 0 , not 10; or 3+ 8 = 1, not 11) consecutively, say, start with 1 and 2; 1 plus 2 = 3, then 2 + 3 = 5, then 3 + 5 = 8, then 5 + 8 = 1, then 8 + 1 = 9, etc., up to the 61st digit. The 61st digit will always repeat the 1st digit you started with.
Great! There was a time when I'd work that out.
Now.... too ....hard ... to .... think....
Post a Comment